Hace poco fue el aniversario del nacimiento de Paul Dirac; además, en el mismo mes de agosto, pero en 1932 (treinta años más tarde del nacimiento de Dirac), se encontraría evidencia experimental de la existencia del positrón, tan sólo dos años más tarde de que Dirac (auténticamente) lo predijera.
Sobre la vida de Dirac también está el famoso libro The Strangest Man de Graham Farmelo, que no he tenido oportunidad de leer porque es complicado conseguirlo en México, aunque en YouTube se encuentra esta charla del mismo Farmelo:
De las relaciones de momento-energía clásicas no-relativista y relativista de una partícula podemos obtener sus ecuaciones mecánico-cuánticas a través de la correspondencia $(E,\vec{p})\to(i\p_t,-i\nabla)$ en unidades naturales ($\hbar=c=1$). En el caso no-relativista, con el potencial $V=V(x,t)$, tenemos que
\begin{equation}E=\frac{\vec{p}\cdot\vec{p}}{2m}+V\,\to\,i\p_t=-\frac{\nabla^2}{2m}+\hat{V}\end{equation} que aplicado a una función de onda $\Psi=\Psi(x,t)$, reproduce la ecuación de Schrödinger
\begin{equation}i\p_t\Psi=\left(-\frac{\nabla^2}{2m}+\hat{V}\right)\Psi\end{equation} y de manera análoga se puede tomar (el cuadrado de) la relación relativista $E^2=p^2+m^2$ de modo que
\begin{equation}\left(-\p_t^2+\nabla^2-m^2\right)\Psi=0\end{equation} que es la ecuación de Klein-Gordon. Finalmente, como se hace con la ecuación de Schödinger, se puede obtener una densidad de probabilidad (que junto con la corriente de probabilidad satisfacen una ecuación de continuidad), que sin embargo para este caso no es positiva definida.
En su artículo The Quantum Theory of the Electron de febrero de 1928, Dirac abordó principalmente este problema para electrones considerando que la ecuación cuántico-relativista debía ser lineal o de primer orden en $\p_t$. Dirac es seguramente uno de los autores de antaño que es más sencillo de leer y su famoso artículo no es la excepción. Resumiendo, Dirac parte de que en relatividad especial la dirección temporal "está al mismo nivel" que las demás, de modo que si la ecuación dinámica es lineal en $\p_t$ (i.e. $p_0$), también tendría que serlo en $\p_i$ (i.e. $p_i$), de donde propone la ecuación de prueba (o ansatz)
\begin{equation}\left(p_0+\alpha^ip_i+\beta\right)\Psi=0\end{equation} que debe además ser compatible con la relación de energía-momento relativista, i.e. debe reproducir la ecuación de Klein-Gordon (interpretada como un límite clásico --large quantum numbers) si se eleva al cuadrado el lado izquierdo, de donde obtiene relaciones de las que se sigue que los $\alpha_\mu$ no pueden ser números ordinarios y pueden representarse por matrices. Dirac luego construye un caso particular de estas matrices en lo que hoy conocemos como una representación del álgebra de Clifford. Concretamente, en notación moderna (Dirac la escribe también de forma parecida cuando demuestra que la ecuación es invariante ante transformaciones de Lorentz),
\begin{equation}\left(i\gamma^\mu\p_\mu-m\right)\psi=0\end{equation} es la ecuación de Dirac con $\{\gamma^\mu,\gamma^\nu\}=\gamma^\mu\gamma^\nu+\gamma^\nu\gamma^\mu=2\eta^{\mu\nu}\mathbb{I}$ el álgebra de Clifford (Dirac encuentra una representación particular, notando antes que cualquiera debe estár formada por matrices de al menos 4x4) y $\psi$ es un 4-vector, que concretamente en teoría cuántica de campos se conoce como espinor (aunque desde antes se conocía así precisamente por poderse relacionar con el espín de los electrones).
De su ecuación, Dirac resolvió el problema de la densidad de probabilidad negativa [otra forma de determinar los coeficientes de la ecuación de Dirac es precisamente buscando que se satisfaga una ecuación de continuidad de tipo $\p_t(\psi^\dagger\psi)+\nabla\cdot\vec{j}=0$] pero persistía otro problema importante: energías negativas. Resulta que las soluciones de la ecuación de Dirac pueden descomponerse en dos espinores de dos componentes que son eigenestados de energía positiva y negativa. Clásicamente las energías negativas pueden simplemente ignorarse por no tener sentido físico y nada impide descartarlas, de cualquier modo en cuántica estos estados no pueden ignorarse así nada más, ya que la teoría misma requiere tener conjuntos completos (y ortonormales) de eigenestados.
Así pues, Dirac, viendo al monstruo que había creado, atacó también de manera bastante ingeniosa este problema en el artículo A Theory of Electrons and Protons: los electrones son fermiones, así que están sujetos al principio de exclusión de Pauli y por tanto los estados de energía negativa deben estar todos ocupados, siendo accesibles únicamente los de energía positiva. Esto es lo que se conoce como el mar de Dirac. Pero Dirac no se detuvo ahí, notó además que un hueco en el mar de Dirac se comporta como una partícula con carga positiva y el resto de propiedades del electrón: el antielectrón o positrón, que además se aniquila con el electrón emitiendo radiación.
Finalmente el mar de Dirac resultó ser sólo una pifia, de cualquier modo, increíblemente llevó a la respuesta correcta sobre el positrón y luego en general sobre la antimateria. Hoy (y desde algo así como 1934) la ecuación de Dirac únicamente se entiende consistentemente en el contexto de la teoría cuántica de campos: el espinor no es una función de onda, sino un campo clásico que se cuantiza en partículas de espín 1/2 y las antipartículas no están asociadas necesariamente sólo a fermiones, además el Hamiltoniano asociado a la ecuación de Dirac es positivo definido, de modo que es acotado por abajo, como debe, y desaparecen las energías negativas. De manera análoga, más tarde la ecuación de Klein-Gordon fue interpretada por Pauli (?) como una para un campo de espín nulo, también con un Hamiltoniano positivo definido y energías positivas.
Y la idea es bastante simple: utilizar una cámara de niebla: un detector de partículas que funciona mediante vapor de agua supersaturado. El vapor de la cámara de niebla se ioniza cuando cierta radiación ionizante pasa por él, en este caso rayos cósmicos (apenas descubiertos), lo que genera el rastro de un camino ionizado que se fotografía para ser analizado. Si además se aplica un campo magnético, las partículas se curvarán en cierta dirección debido a la fuerza de Lorentz.
A fin de cuentas Anderson encontró que la partícula que estaba midiendo no podía ser un protón y que correspondía al electrón de carga positiva, que bautizó como positrón. Y el resto es historia, se siguieron descubriendo antipartículas y se generó la noción de la antimateria, que puede ser tan estigmatizada por la cantidad de energía que libera al aniquilarse con la materia hasta ser tan mundana por aplicaciones como la tomografía por emisión de positrones.
Happy birthday to quantum pioneer and the "strangest man," Paul Dirac! #physics pic.twitter.com/uxM6wfo8Jj— Perimeter Institute (@Perimeter) August 8, 2015Sobre la vida de Dirac también está el famoso libro The Strangest Man de Graham Farmelo, que no he tenido oportunidad de leer porque es complicado conseguirlo en México, aunque en YouTube se encuentra esta charla del mismo Farmelo:
De las relaciones de momento-energía clásicas no-relativista y relativista de una partícula podemos obtener sus ecuaciones mecánico-cuánticas a través de la correspondencia $(E,\vec{p})\to(i\p_t,-i\nabla)$ en unidades naturales ($\hbar=c=1$). En el caso no-relativista, con el potencial $V=V(x,t)$, tenemos que
\begin{equation}E=\frac{\vec{p}\cdot\vec{p}}{2m}+V\,\to\,i\p_t=-\frac{\nabla^2}{2m}+\hat{V}\end{equation} que aplicado a una función de onda $\Psi=\Psi(x,t)$, reproduce la ecuación de Schrödinger
\begin{equation}i\p_t\Psi=\left(-\frac{\nabla^2}{2m}+\hat{V}\right)\Psi\end{equation} y de manera análoga se puede tomar (el cuadrado de) la relación relativista $E^2=p^2+m^2$ de modo que
\begin{equation}\left(-\p_t^2+\nabla^2-m^2\right)\Psi=0\end{equation} que es la ecuación de Klein-Gordon. Finalmente, como se hace con la ecuación de Schödinger, se puede obtener una densidad de probabilidad (que junto con la corriente de probabilidad satisfacen una ecuación de continuidad), que sin embargo para este caso no es positiva definida.
En su artículo The Quantum Theory of the Electron de febrero de 1928, Dirac abordó principalmente este problema para electrones considerando que la ecuación cuántico-relativista debía ser lineal o de primer orden en $\p_t$. Dirac es seguramente uno de los autores de antaño que es más sencillo de leer y su famoso artículo no es la excepción. Resumiendo, Dirac parte de que en relatividad especial la dirección temporal "está al mismo nivel" que las demás, de modo que si la ecuación dinámica es lineal en $\p_t$ (i.e. $p_0$), también tendría que serlo en $\p_i$ (i.e. $p_i$), de donde propone la ecuación de prueba (o ansatz)
\begin{equation}\left(p_0+\alpha^ip_i+\beta\right)\Psi=0\end{equation} que debe además ser compatible con la relación de energía-momento relativista, i.e. debe reproducir la ecuación de Klein-Gordon (interpretada como un límite clásico --large quantum numbers) si se eleva al cuadrado el lado izquierdo, de donde obtiene relaciones de las que se sigue que los $\alpha_\mu$ no pueden ser números ordinarios y pueden representarse por matrices. Dirac luego construye un caso particular de estas matrices en lo que hoy conocemos como una representación del álgebra de Clifford. Concretamente, en notación moderna (Dirac la escribe también de forma parecida cuando demuestra que la ecuación es invariante ante transformaciones de Lorentz),
\begin{equation}\left(i\gamma^\mu\p_\mu-m\right)\psi=0\end{equation} es la ecuación de Dirac con $\{\gamma^\mu,\gamma^\nu\}=\gamma^\mu\gamma^\nu+\gamma^\nu\gamma^\mu=2\eta^{\mu\nu}\mathbb{I}$ el álgebra de Clifford (Dirac encuentra una representación particular, notando antes que cualquiera debe estár formada por matrices de al menos 4x4) y $\psi$ es un 4-vector, que concretamente en teoría cuántica de campos se conoce como espinor (aunque desde antes se conocía así precisamente por poderse relacionar con el espín de los electrones).
De su ecuación, Dirac resolvió el problema de la densidad de probabilidad negativa [otra forma de determinar los coeficientes de la ecuación de Dirac es precisamente buscando que se satisfaga una ecuación de continuidad de tipo $\p_t(\psi^\dagger\psi)+\nabla\cdot\vec{j}=0$] pero persistía otro problema importante: energías negativas. Resulta que las soluciones de la ecuación de Dirac pueden descomponerse en dos espinores de dos componentes que son eigenestados de energía positiva y negativa. Clásicamente las energías negativas pueden simplemente ignorarse por no tener sentido físico y nada impide descartarlas, de cualquier modo en cuántica estos estados no pueden ignorarse así nada más, ya que la teoría misma requiere tener conjuntos completos (y ortonormales) de eigenestados.
Así pues, Dirac, viendo al monstruo que había creado, atacó también de manera bastante ingeniosa este problema en el artículo A Theory of Electrons and Protons: los electrones son fermiones, así que están sujetos al principio de exclusión de Pauli y por tanto los estados de energía negativa deben estar todos ocupados, siendo accesibles únicamente los de energía positiva. Esto es lo que se conoce como el mar de Dirac. Pero Dirac no se detuvo ahí, notó además que un hueco en el mar de Dirac se comporta como una partícula con carga positiva y el resto de propiedades del electrón: el antielectrón o positrón, que además se aniquila con el electrón emitiendo radiación.
Finalmente el mar de Dirac resultó ser sólo una pifia, de cualquier modo, increíblemente llevó a la respuesta correcta sobre el positrón y luego en general sobre la antimateria. Hoy (y desde algo así como 1934) la ecuación de Dirac únicamente se entiende consistentemente en el contexto de la teoría cuántica de campos: el espinor no es una función de onda, sino un campo clásico que se cuantiza en partículas de espín 1/2 y las antipartículas no están asociadas necesariamente sólo a fermiones, además el Hamiltoniano asociado a la ecuación de Dirac es positivo definido, de modo que es acotado por abajo, como debe, y desaparecen las energías negativas. De manera análoga, más tarde la ecuación de Klein-Gordon fue interpretada por Pauli (?) como una para un campo de espín nulo, también con un Hamiltoniano positivo definido y energías positivas.
In this attempt, the success seems to have been on the side of Dirac rather than logic.La predicción de Dirac seguramente era descabellada, además de que nunca se había reportado la observación experimental de algo parecido. Como sea, y contrario a muchas ideas relevantes actualmente, se tenía la ventaja de que se podía falsificar rápidamente su predicción, y así ocurrió con un experimento de Carl Anderson en 1932.- Pauli sobre Dirac
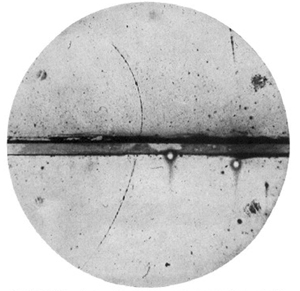 |
| Carl D. Anderson, Physical Review Vol.43, p491 (1933) |
Y la idea es bastante simple: utilizar una cámara de niebla: un detector de partículas que funciona mediante vapor de agua supersaturado. El vapor de la cámara de niebla se ioniza cuando cierta radiación ionizante pasa por él, en este caso rayos cósmicos (apenas descubiertos), lo que genera el rastro de un camino ionizado que se fotografía para ser analizado. Si además se aplica un campo magnético, las partículas se curvarán en cierta dirección debido a la fuerza de Lorentz.
 |
| Producción de un electrón y un positrón a partir de un fotón de alta energía. Fuente: http://teachers.web.cern.ch |
A fin de cuentas Anderson encontró que la partícula que estaba midiendo no podía ser un protón y que correspondía al electrón de carga positiva, que bautizó como positrón. Y el resto es historia, se siguieron descubriendo antipartículas y se generó la noción de la antimateria, que puede ser tan estigmatizada por la cantidad de energía que libera al aniquilarse con la materia hasta ser tan mundana por aplicaciones como la tomografía por emisión de positrones.
When I was a young man, Dirac was my hero. He made a breakthrough, a new method of doing physics. He had the courage to simply guess at the form of an equation, the equation we now call the Dirac equation, and to try to interpret it afterwards. Maxwell in his day got his equations, but only in an enormous mass of 'gear wheels' and so forth.- Feynman en "The Reason for Antiparticles"
No comments:
Post a Comment