Hace poco encontré esta imagen (fuente):

lo que básicamente significa que el hiperboloide de una hoja puede construirse empleando únicamente líneas rectas.
En general, una superficie reglada $\mathcal{S}\subset\mathbb{R}^3$ puede pensarse como una superficie que puede generarse moviendo una línea recta en el espacio (aquí $\mathbb{R}^3$). Esto entonces dice que cualquier superficie reglada tiene una parametrización $\alpha:\mathcal{U}\times\mathcal{V}\to\mathcal{S}$ de la forma
\begin{equation}\alpha(u,v)=\beta(u)\,v+\gamma(u)\end{equation} con $u\in\mathcal{U}$, $v\in\mathcal{V}$ dos parámetros y $\beta,\gamma:\mathcal{U}\to\mathbb{R}^3$ curvas en el espacio. Esto es, algo así como la generalización de una parametrización de la de una recta $y(t)=ax(t)+b$. Se dice además que $\alpha$ es un parche reglado, $\beta$ la curva directriz y $\gamma$ la curva base. Las mismas líneas rectas $v\mapsto\alpha(u_0,v)$ son llamadas reglas (intento de traducción de rulings). Nota que $\beta$ no debe ser cero y que $\gamma$ no debe ser constante para tener una genuina superficie reglada.
Quizá la forma más sencilla de mostrar cómo es que el hiperboloide de una hoja es una superficie reglada es así (fuente):

Se puede construir el parche reglado del hiperboloide de una hoja de manera intuitiva de forma similar a como puede construirse su ecuación cuadrática: pensando en elipses. Una elipse en el plano $\{x,y,0\}$ puede parametrizarse por
\begin{equation}\mathcal{E}(u)=(a\cos{u},b\sin{u},0),\hspace{0.5in}u\in[0,2\pi)\equiv\mathcal{U}\end{equation} y convenientemente podemos elegir a $\mathcal{E}$ como la curva base. La ecuación cuadrática del hiperboloide de una hoja es
\begin{equation}\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1\end{equation} con $a,b,c>0$ constantes. Entonces queremos encontrar el parche reglado
\begin{equation}\mathcal{H}(u,v)\equiv\beta(u)\,v+\mathcal{E}(u)=\left(\mathcal{H}_x(u,v),\mathcal{H}_y(u,v),\mathcal{H}_z(u,v)\right)\end{equation} con $v\in\mathbb{R}\equiv\mathcal{V}$ y tal que
\begin{equation}\mathcal{H}_x^2+\mathcal{H}_y^2-\mathcal{H}_z^2=1\end{equation} es decir, si $\beta(u)=(\beta_x(u),\beta_y(u),\beta_z(u))$,
\begin{equation}\frac{\beta_x^2v^2}{a^2}+\frac{\beta_y^2v^2}{b^2}+\frac{2}{a}\beta_xv\cos{u}+\frac{2}{b}\beta_yv\sin{u}=\frac{\beta_z^2}{c^2}v^2\end{equation} de donde requerimos que el lado izquierdo sea proporcional a $v^2$ pues por definición $\beta_z=\beta_z(u)$, o la parametrización, aunque seguiría siendo válida, ya no sería un parche reglado. El lector puede investigar, si así lo desea, qué elecciones $\beta_x,\beta_y$ hay de modo que esto ocurra, pero si no se tiene la paciencia y el tiempo para hacer los pasos algebráicos, la elección más sencilla y evidente es
\begin{equation}\beta_x=\pm{a}\sin{u},\hspace{0.5in}\beta_y=\mp{b}\cos{u}\end{equation} de modo que se siga que
\begin{equation}\beta_z=c\end{equation} y finalmente entonces
\begin{equation}\mathcal{H}_\pm(u,v)=\left(a(\cos{u}\pm{v}\sin{u}),b(\sin{u}\mp{v}\cos{u}),cv\right)\end{equation} que son de hecho dos parches reglados distintos y en consecuencia se dice que el hiperboloide de dos hojas es una superficie doblemente reglada. Algunas visualizaciones que hice con Mathematica son las que siguen:
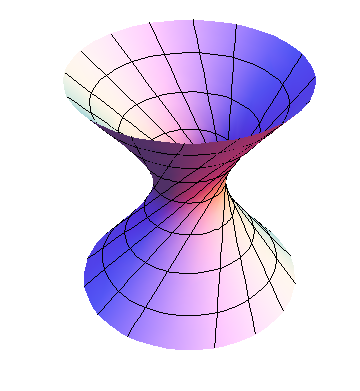
 Tomando $u\in[0,u_f)$ y modificando $u_f$ hasta $2\pi$,
Tomando $u\in[0,u_f)$ y modificando $u_f$ hasta $2\pi$,


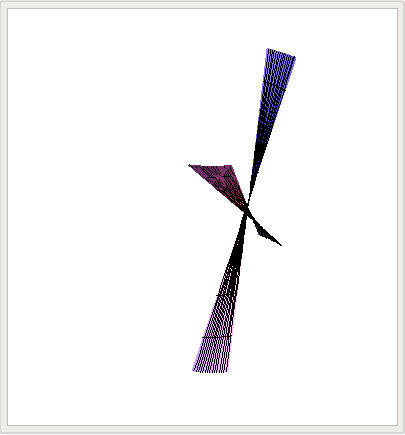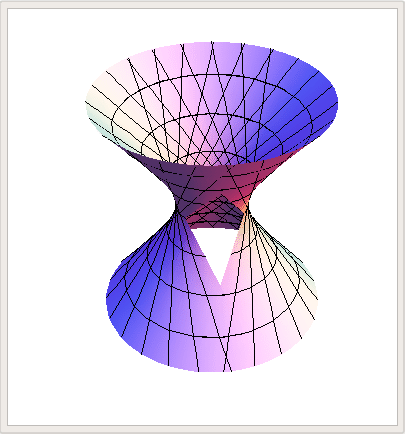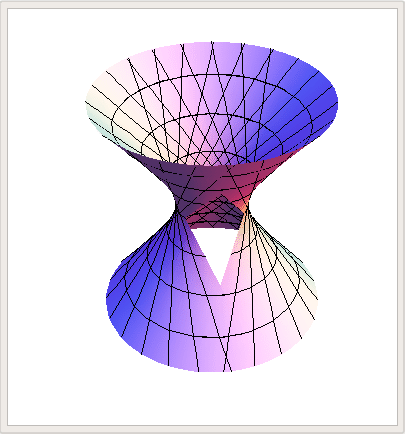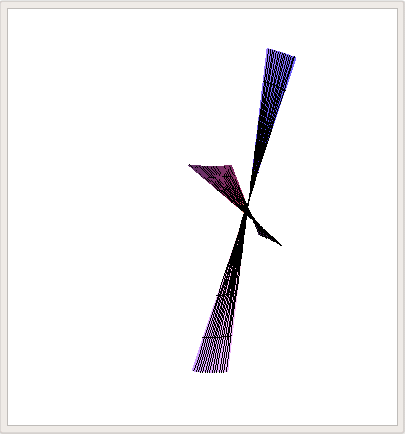
o bien, en el espíritu del primer GIF, cambiando valores constantes de $u_0\in[0,2\pi)$ y graficando las rectas $v\mapsto\mathcal{H}_+(u_0,v)$,

También es interesante que se puede escribir
\begin{equation}\mathcal{H}_\pm(u,v)=\pm\mathcal{E}^\prime(u){v}+\mathcal{E}(u)\pm(0,0,cv)\end{equation} y uno puede visualizar cómo cambia la superficie y su proyección en el plano $\{x,y,0\}$ en el parámetro $v$.
Las únicas superficies doblemente regladas son el plano, el paraboloide hiperbólico (silla de montar) y el hiperboloide de una hoja. En general los conos y los cilindros son las superficies regladas más sencillas y también en general las superficies regladas suelen ser las más sencillas de parametrizar. Hay también por supuesto un sinfín de propiedades de estas superficies que pueden estudiarse, además, por supuesto, de que en el caso tridimensional resultan visualmente atractivas y pueden ser de gran utilidad para diseñadores, arquitectos, etc...
Finalmente, hay por supuesto otras superficies regladas más complicadas (e.g. el conoide de Plücker), pero ya que estoy con esto de visualizaciones y pequeños GIF's animados con Mathematica, dejaré más de una superficie reglada muy famosa: la cinta de Möbius parametrizada por
\begin{equation}\mathcal{M}(u,v)=\left(\cos{u/2}\,\cos{u},\cos{u/2}\sin{u},\sin{u/2}\right)\,v+(\cos{u},\sin{u},0)\end{equation}

lo que básicamente significa que el hiperboloide de una hoja puede construirse empleando únicamente líneas rectas.
En general, una superficie reglada $\mathcal{S}\subset\mathbb{R}^3$ puede pensarse como una superficie que puede generarse moviendo una línea recta en el espacio (aquí $\mathbb{R}^3$). Esto entonces dice que cualquier superficie reglada tiene una parametrización $\alpha:\mathcal{U}\times\mathcal{V}\to\mathcal{S}$ de la forma
\begin{equation}\alpha(u,v)=\beta(u)\,v+\gamma(u)\end{equation} con $u\in\mathcal{U}$, $v\in\mathcal{V}$ dos parámetros y $\beta,\gamma:\mathcal{U}\to\mathbb{R}^3$ curvas en el espacio. Esto es, algo así como la generalización de una parametrización de la de una recta $y(t)=ax(t)+b$. Se dice además que $\alpha$ es un parche reglado, $\beta$ la curva directriz y $\gamma$ la curva base. Las mismas líneas rectas $v\mapsto\alpha(u_0,v)$ son llamadas reglas (intento de traducción de rulings). Nota que $\beta$ no debe ser cero y que $\gamma$ no debe ser constante para tener una genuina superficie reglada.
Quizá la forma más sencilla de mostrar cómo es que el hiperboloide de una hoja es una superficie reglada es así (fuente):

Se puede construir el parche reglado del hiperboloide de una hoja de manera intuitiva de forma similar a como puede construirse su ecuación cuadrática: pensando en elipses. Una elipse en el plano $\{x,y,0\}$ puede parametrizarse por
\begin{equation}\mathcal{E}(u)=(a\cos{u},b\sin{u},0),\hspace{0.5in}u\in[0,2\pi)\equiv\mathcal{U}\end{equation} y convenientemente podemos elegir a $\mathcal{E}$ como la curva base. La ecuación cuadrática del hiperboloide de una hoja es
\begin{equation}\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1\end{equation} con $a,b,c>0$ constantes. Entonces queremos encontrar el parche reglado
\begin{equation}\mathcal{H}(u,v)\equiv\beta(u)\,v+\mathcal{E}(u)=\left(\mathcal{H}_x(u,v),\mathcal{H}_y(u,v),\mathcal{H}_z(u,v)\right)\end{equation} con $v\in\mathbb{R}\equiv\mathcal{V}$ y tal que
\begin{equation}\mathcal{H}_x^2+\mathcal{H}_y^2-\mathcal{H}_z^2=1\end{equation} es decir, si $\beta(u)=(\beta_x(u),\beta_y(u),\beta_z(u))$,
\begin{equation}\frac{\beta_x^2v^2}{a^2}+\frac{\beta_y^2v^2}{b^2}+\frac{2}{a}\beta_xv\cos{u}+\frac{2}{b}\beta_yv\sin{u}=\frac{\beta_z^2}{c^2}v^2\end{equation} de donde requerimos que el lado izquierdo sea proporcional a $v^2$ pues por definición $\beta_z=\beta_z(u)$, o la parametrización, aunque seguiría siendo válida, ya no sería un parche reglado. El lector puede investigar, si así lo desea, qué elecciones $\beta_x,\beta_y$ hay de modo que esto ocurra, pero si no se tiene la paciencia y el tiempo para hacer los pasos algebráicos, la elección más sencilla y evidente es
\begin{equation}\beta_x=\pm{a}\sin{u},\hspace{0.5in}\beta_y=\mp{b}\cos{u}\end{equation} de modo que se siga que
\begin{equation}\beta_z=c\end{equation} y finalmente entonces
\begin{equation}\mathcal{H}_\pm(u,v)=\left(a(\cos{u}\pm{v}\sin{u}),b(\sin{u}\mp{v}\cos{u}),cv\right)\end{equation} que son de hecho dos parches reglados distintos y en consecuencia se dice que el hiperboloide de dos hojas es una superficie doblemente reglada. Algunas visualizaciones que hice con Mathematica son las que siguen:




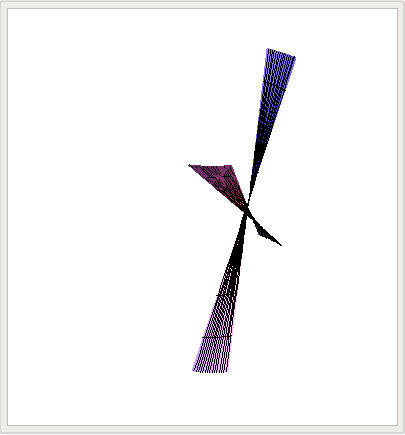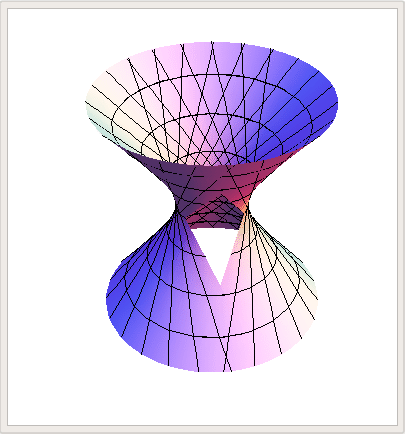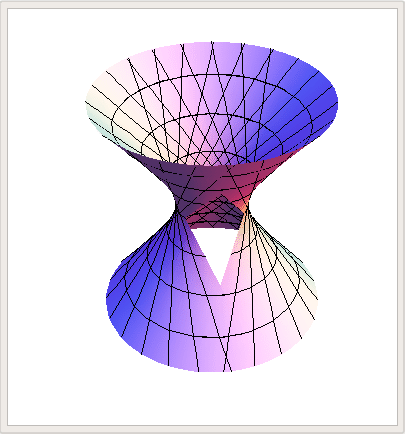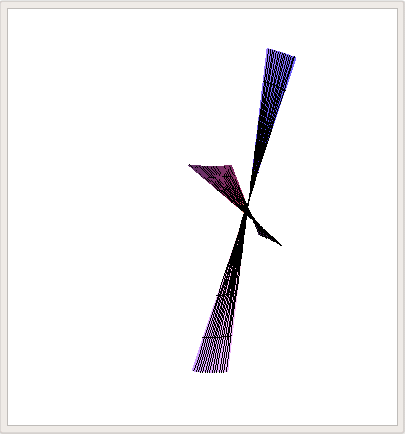
o bien, en el espíritu del primer GIF, cambiando valores constantes de $u_0\in[0,2\pi)$ y graficando las rectas $v\mapsto\mathcal{H}_+(u_0,v)$,

También es interesante que se puede escribir
\begin{equation}\mathcal{H}_\pm(u,v)=\pm\mathcal{E}^\prime(u){v}+\mathcal{E}(u)\pm(0,0,cv)\end{equation} y uno puede visualizar cómo cambia la superficie y su proyección en el plano $\{x,y,0\}$ en el parámetro $v$.
 |
| $\mathcal{H}_+(u,v)$ y cambiando $v$ de -6 a 6 |
 |
| $\mathcal{E}^\prime(u)v+\mathcal{E}(u)$ y cambiando $v$ de 0 a 6 |
Las únicas superficies doblemente regladas son el plano, el paraboloide hiperbólico (silla de montar) y el hiperboloide de una hoja. En general los conos y los cilindros son las superficies regladas más sencillas y también en general las superficies regladas suelen ser las más sencillas de parametrizar. Hay también por supuesto un sinfín de propiedades de estas superficies que pueden estudiarse, además, por supuesto, de que en el caso tridimensional resultan visualmente atractivas y pueden ser de gran utilidad para diseñadores, arquitectos, etc...
 |
| Estación de tren en Varsovia, Polonia: Paraboloide Hiperbólico (fuente) |
\begin{equation}\mathcal{M}(u,v)=\left(\cos{u/2}\,\cos{u},\cos{u/2}\sin{u},\sin{u/2}\right)\,v+(\cos{u},\sin{u},0)\end{equation}
 |
| La curva directriz de la banda de Möbius recorrida en sentido positivo en $u\in[-2\pi,2\pi)$ y contenida en la 2-esfera unitaria |
 |
| Tomando $v\in[-1/2,1/2]$, $u\in[0,u_f)$ y modificando $u_f$ hasta $2\pi$ |
No comments:
Post a Comment