El 2015 ha sido llamado el año de la luz, y un hecho acerca de ésta que toda persona debe saber es que tiene una velocidad constante. Hace poco me encontré el siguiente vídeo de Brian Greene, en donde explica con su estilo excepcionalmente claro a qué nos referimos cuando decimos que la velocidad de la luz es constante. Lamento que el vídeo esté en inglés, pero la explicación de Greene se reduce a esto: no importa cómo la midamos, ya sea acercándonos o alejándonos rápidamente de ella, siempre medimos el mismo valor, a diferencia de cuando medimos la velocidad de otros objetos como por ejemplo de una pelota. Estrictamente cuando decimos ésto, los físicos estamos pensando en que la velocidad es constante para cualquier sistema de referencia inercial... pero por el momento esto son detalles extra; acá más información, o bien al final de esta entrada ;-)
Hasta acá la cosa parece bastante sencilla, pero este hecho tan simple tiene consecuencias que cambiaron para siempre nuestra percepción de la naturaleza del espacio y el tiempo con el nacimiento de la relatividad especial de Einstein en 1905, desde el hecho de que 'nada' viaja más rápido que la luz (entre otras causas por la llamada causalidad, aunque no lo discutiré acá) hasta algunos de los efectos más sorprendentes como que el espacio puede contraerse y el tiempo dilatarse.
La motivación de Einstein
Vale, pues usualmente se dice que esta 'invariancia' de la velocidad de la luz es un postulado de la relatividad especial, es decir, algo que se propone a priori y se emplea para poder formular la teoría, ¿pero entonces cómo es que se le ocurrió a Einstein proponer este postulado que dice que la velocidad de la luz es constante?
Greene también tiene un buen vídeo con la explicación: la teoría del electromagnetismo de Maxwell parecía sugerir que la velocidad de la luz es constante, lo que implicaba que el espacio y el tiempo se tendrían que comportar de manera distinta a la que nos es usual.
Pues... por ahí va la cosa.
Un ejercicio obligado en las clases de electromagnetismo clásico de licenciatura es el de encontrar, a partir de las ecuaciones de Maxwell, que los campos eléctrico y magnético satisfacen respectivas ecuaciones de onda que se propagan con una velocidad de poquitín menos de 300,000,000 m/s ([1]); estas ondas están sincronizadas en lo que se conoce clásicamente como radiación electromagnética, o simplemente, luz. Vale, entonces si éste es el valor de la velocidad de propagación de la luz en el marco de referencia en que lo deducen los alumnos, debería ser el mismo en cualquier otro (de hecho el marco 'elegido' implícitamente por los alumnos es desde un principio arbitrario); a fin de cuentas Galileo nos enseñó que las leyes de la física son las mismas independientemente de si las vemos en algún punto del espacio u otro o de si nos movemos con una velocidad constante de uno u otro modo.
El genio de Einstein para investigar esta cuestión sobre la velocidad de la luz fue precisamente el de tomar este principio de invariancia de las leyes físicas de Galileo en serio (que se llama principio de relatividad básicamente porque propone esta invariancia respecto a movimientos relativos entre marcos de referencia) y el de llevarlo a sus últimas consecuencias a pesar de los efectos poco intuitivos que acarreó en el entendimiento del espacio y el tiempo.
Cuando los físicos querían ver las ecuaciones de una onda electromagnética (o en general las ecuaciones de Maxwell) en otros sistemas de referencia, particularmente en uno que se mueve a velocidad constante, obtenían versiones distintas ([2]), lo que sugería que la luz no se propagaba siempre de la misma forma y con la misma velocidad, además de implicar que existían marcos de referencia privilegiados en los que las ecuaciones son todas bellas como Maxwell las describió originalmente [ignoro quiénes eran esos físicos, pero vaya, el dilema era esencialmente éste ;-)]. Los físicos por supuesto comenzaron a proponer soluciones a este problema, entre ellas la famosa solución del éter, que de hecho parecía bastante natural dada la idea de que una onda o vibración requiere de un medio para propagarse. Albert Michelson y Edward Morley realizaron un famoso experimento en 1887 en el que compararon la velocidad de la luz en distintas direcciones y básicamente encontraron que esta velocidad siempre es apróx. 300,000,000 m/s en cualquier dirección, descartando casi sin querer, la propuesta del éter. A la vista de estos resultados y de otros efectos relacionados como el efecto Doppler, el experimento de Fizeau y la aberración de la luz, grandes físicos como Poincaré, y antes Larmor y Lorentz, buscaron dar una explicación (algunos, como los mencionados, aferrándose al mismo éter) y de hecho hicieron grandes avances; de cualquier modo, no fue sino hasta Einstein cuando realmente se comprendieron las implicaciones de la invariancia de la velocidad de la luz y el principio de relatividad de Galileo en la naturaleza misma del espacio-tiempo.
La gran idea, y algo así como el 'sistema operativo', de la relatividad especial que dio solución al problema es la de las llamadas transformaciones de Lorentz, en la que precisamente trabajaron de manera fundamental (y en ese sentido hicieron avances) Poincaré, Larmor y Lorentz antes de Einstein. Una transformación en un sentido matemático no es más que una función que relaciona puntos de un espacio con otros puntos dentro del mismo espacio: las rotaciones, las traslaciones y los desplazamientos a velocidad constante de marcos de referencia son ejemplos de transformaciones y son éstas precisamente las transformaciones que mantienen la invariancia Galileana de las leyes físicas, por lo que a todas ellas juntas se les llama transformaciones Galileanas; el caso de los desplazamientos a velocidad constante es el que daba problemas cuando se quería considerar en el electromagnetismo (Greene explica el proceso matemático junto con la idea de simetría en este vídeo, aunque en el contexto del bosón de Higgs). En particular cuando uno considera estos desplazamientos a velocidad constante en las ecuaciones de onda del electromagnetismo, lo que se encuentra es que a velocidades bajas respecto a la de la luz, las ecuaciones se ven prácticamente igual a las originales pero no así cuando la velocidad de movimiento del marco de referencia respecto a la de la luz es alta ([3]). Cuando se habla de las transformaciones de Lorentz, se habla de rotaciones de marcos de referencia y de un tipo especial de transformación llamada boost que es análogo a los desplazamientos a velocidad constante; de este modo, las transformaciones de Lorentz se hacen cargo del problema generalizando los desplazamientos a velocidad constante con los boosts, que son válidos para desplazamientos a velocidades cercanas a la de la luz y que a su vez se reducen a los desplazamientos à la Galileo a velocidades bajas, lo que hace también que la relatividad especial sea una forma generalizada de la mecánica clásica y de este modo sea enteramente consistente.
El título de 'transformaciones de Lorentz' presuntamente lo acuñó Poincaré, pero bien podrían llamarse de Voigt-Larmor-Lorentz-Poincaré-Einstein ([4]) ;-) finalmente el éxito de Einstein fue que derivó y entendió estas transformaciones físicamente como relaciones espacio-temporales y dedujo las consecuencias revolucionarias (entre otras) de la dilatación temporal y la contracción espacial, que básicamente significaron que el espacio y el tiempo dejaran de ser algo absoluto y universal, mientras que la velocidad de la luz es exactamente la misma sin importar 'cómo se le vea'. Poco tiempo después otro desarrollo importante, también impulsado por Poincaré pero finalizado por Minkowski, fue el de que el espacio y el tiempo están íntimamente unidos en un espacio 4-dimensional, no Euclideano (o que puede pensarse con la coordenada temporal siendo imaginaria) que ahora llamamos espacio-tiempo (lo que a veces se atribuye directamente a Einstein), en donde los boosts son vistos como rotaciones espacio-temporales y en el que la relatividad especial (y el electromagnetismo) se formula naturalmente.
Finalmente algo tentador es pensar que la invariancia de la velocidad de la luz no debería ser algo que se propone a priori, sino que debe deducirse como consecuencia de la teoría. Y en cierto sentido es cierto, ya que puede obtenerse que la velocidad de la luz es finita únicamente a partir del principio de relatividad de Galileo y deducir que es constante del electromagnetismo clásico o de otras propiedades de simetría, pero la cuestión se torna en algo parecido a la discusión sobre si la primera ley de Newton es un caso particular de la segunda; el hecho es que ambas formas son válidas e incluso posiblemente el deducirlo es la mejor forma de hacerlo desde un punto de vista moderno (donde la luz es simplemente un campo más), de cualquier modo todo parece sencillo cuando se conoce de antemano cuál es la solución ;-)
¿Y si la luz viaja en un medio?
Seguido se dice que la luz en un medio viaja más lentamente que en el vacío, pero esto así dicho nada más no es estrictamente correcto tomando en cuenta todo lo anterior y puede resultar engañoso; en general no es correcto tampoco decir que la luz puede detenerse o que puede hacerse disminuir su velocidad. Lo que sí se puede decir sin meter la pata es que se puede hacer que la luz recorra una cierta distancia en un tiempo menor o bien que la luz se puede propagar más lentamente en un medio; de cualquier modo la distinción puede resultar un poco pedante e incluso pasar desapercibida en la distinción que lleva implícita.
Como sea es relevante aclarar lo que sucede cuando la luz se propaga en un medio.
Clásicamente la luz está descrita por una onda electromagnética; así como uno obtiene el valor para la velocidad de propagación de la luz en el vacío, uno puede obtener una expresión para la velocidad de propagación de la luz en un medio dado (aunque de forma algo más complicada que en [1]) a través de las propiedades eléctricas y magnéticas que describen clásicamente al medio. La imagen macroscópica de esto último que uno tendría sería simplemente la de una onda viajando más lentamente al entrar en el medio.

Pensando a nivel atómico [sin invocar los detalles de la mecánica cuántica, es decir, pensando sólo en esferitas pequeñitas ;-) ], si se considera un medio con materia cualquiera [sólo no pensemos en nada exótico por el momento] que a fin de cuentas no está compuesto más que por átomos que a su vez no son más un núcleo y electrones, como es de imaginarse, pasa que la luz puede interactuar con la materia del medio, es decir, los átomos pueden 'absorber' la energía de la luz, lo que se traduce en 'excitar' o hacer vibrar a los electrones, que cuando se relajan nuevamente liberan esta energía en forma de otro paquete de ondas idéntico. Esto por supuesto no ocurre de manera instantánea, lo que generalizado a una gran cantidad de átomos, causa la ralentización que percibimos a nivel macroscópico. La idea, gráficamente, es ésta:
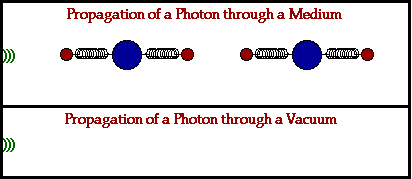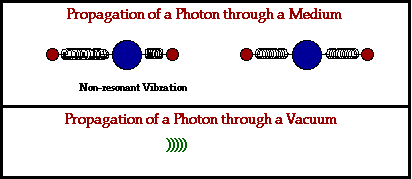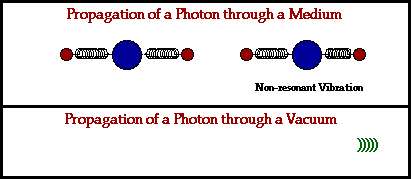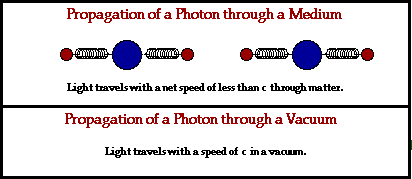
Es decir, es esta interacción con la materia lo que hace que la luz se propague más lentamente en el medio, pero esto no significa que la luz (que puede pensarse también como partículas sin masa, o fotones) deje de viajar a apróx. 300,000,000 m/s. Es por ello que el uso de la palabra propagación es en cierto sentido uno más certero. Si se quiere se puede apelar también a la vieja idea de que un átomo es en su gran mayoría espacio vacío, aunque esto tampoco es del todo correcto [uno puede seguirse con detalles y más detalles ;-) pero la idea principal es ésta].
Un caso exótico de un medio de propagación que resulta interesante en este sentido y que se ha vuelto accesible en tiempos recientes es el de los condensados de Bose-Einstein y la materia ultrafría. En este caso la idea de la absorción y re-emisión de luz también aplica aunque en una forma extrema, como en la llamada 'Transparencia Inducida por Electromagnetismo', logrando reducir la velocidad de propagación de la luz a hasta e.g. 17 m/s.
Otro caso que también es interesante es el de la radiación de Cherenkov, en la que una partícula cargada viaja a una velocidad mayor que la de la propagación de la luz en un medio, lo que ahora el lector debe entender que es enteramente posible respecto a la relatividad especial.
La velocidad de la luz cerca de un agujero negro
Finalmente está el caso en que la relatividad especial no protege la invariancia de la velocidad de la luz: los sistemas de referencia no-inerciales. Un sistema de referencia no inercial es uno que experimenta aceleración respecto a otro sistema de referencia inercial cualquiera. Debo aclarar que eso no significa que la relatividad especial no sirva para describir la dinámica de observadores acelerados (de hecho es necesario que pueda hacerlo para permitir pasar a la relatividad general), pues básicamente lo hace utilizando 'cadenas locales' de observadores inerciales que se mueven instantáneamente, pero esa es otra discusión... detalles ;-)
Como sea, que la velocidad de la luz no sea constante para sistemas no-inerciales es una respuesta incompleta y no con mucho sentido: la cuestión es un tanto más sutil.
La idea clave de la relatividad general (la versión extendida de la relatividad especial que incluye gravedad) que impulsó a Einstein a formularla es el llamado Principio de Equivalencia. Lo que dice este principio es que un observador en reposo dentro de un campo gravitacional es indistinguible de uno acelerado en ausencia de gravedad (de ahí la importancia de que la relatividad especial pueda lidiar con aceleraciones). Esto tiene grandes consecuencias, entre ellas, que la gravedad, antes interpretada como una fuerza o interacción a distancia, no es más que un cambio en la propia geometría del espaciotiempo que altera las trayectorias inerciales acelerándolas. En particular, la gravedad no es más que la expresión de la curvatura del espaciotiempo (que Einstein además luego relacionó con el contenido de energía y materia del espacio).
Así pues, la velocidad de la luz no es siempre constante y puede cambiar cuando uno la mide en espacios curvos, o intuitivamente (en lenguaje Newtoniano, pues), cuando viaja dentro de un campo gravitacional...
¿Por qué tiene poco sentido?
En ausencia de gravedad, la teoría general de la relatividad se reduce al caso especial, en el que el espaciotiempo es plano. Otra forma de plantear el principio de equivalencia es diciendo que cualquier parte de un espaciotiempo curvo siempre ve localmente como un espaciotiempo plano. La palabra mágica local significa 'cerca' o a distancias 'cortas' del origen del observador. Los dos parafraseos del principio de equivalencia toman sentido con el ejemplo de un hombre (en la Tierra) dentro de un elevador cuyos cables se rompen súbitamente, quedando en caída libre, y que no puede distinguir su situación de la de, por ejemplo, un astronauta en el espacio; esto es, un hombre en caída libre experimenta exactamente lo mismo que un observador en el espacio libre de toda 'fuerza' externa. También sabemos por experiencia propia que a distancias cortas el mundo puede ser descrito bastante bien por la mecánica de Newton [o los ingenieros no podrían hacer nada de nada ;-) ], que a su vez utiliza geometría plana; lo único que nos recuerda que estamos en un campo gravitacional es el suelo de la Tierra misma que nos impide experimentar una caída libre todo el tiempo.
Matemáticamente la idea es que el espaciotiempo es algo así como una superficie 4-dimensional llamada variedad (en inglés manifold) que tiene la propiedad de que puede construirse con un montón de 'parches' planos, algo así como una piñata casera que se cubre con pedazos de papel 'planos'.

El decir, pues, que "la velocidad de la luz cambia cuando uno la mide en espacios curvos" es más una declaración de la geometría global del espaciotiempo curvo que de la realidad física acerca de la velocidad de la luz. En el caso de un agujero negro, el que la velocidad de la luz sea nula en el horizonte de eventos, es sólo una afirmación de las coordenadas que lo describen, y puede servir también para señalar que el horizonte de eventos es sólo una singularidad aparente o de coordenadas, y no una singularidad esencial, como la que se encuentra en el interior del agujero negro y en donde la relatividad general simplemente deja de ser válida.
Finalmente toda esta cuestión sirve de recordatorio de que las teorías físicas siempre (al menos hasta ahora) tienen un rango limitado de aplicabilidad, y al menos hasta donde he mostrado aquí, la invariancia de la velocidad de la luz es válida. De cualquier modo el trabajo de los físicos, y los científicos en general, es seguir expandiendo las fronteras de lo que entendemos de la naturaleza como válido ;-)
Las acotaciones
[1] De las ecuaciones de Maxwell en el vacío (sin fuentes)
\begin{align}\nabla\times\mathbf{E}&=-\partial_t\mathbf{B}\\\nabla\times\mathbf{B}&=\mu_0\epsilon_0\partial_t\mathbf{E}\\\nabla\cdot\mathbf{E}&=0\\\nabla\cdot\mathbf{B}&=0\end{align} empleando $\nabla\times(\nabla\times)=\nabla(\nabla\cdot)-\nabla^2$ en los rotacionales, se obtiene que $\left(\mu_0\epsilon_0\partial^2_t-\nabla^2\right)\begin{pmatrix}\mathbf{E}\\\mathbf{B}\end{pmatrix}=0$ de donde se identifica la velocidad de propagación $c=\frac{1}{\sqrt{\mu_0\epsilon_0}}\approx3\times10^8\,\text{m/s}$.
[2], [3] Se considera una transformacion Galileana en dos dimensiones (por simplicidad),
\begin{align}x&\to{x-vt}\\t&\to{t}\end{align} para una ecuación de onda clásica cualquiera con velocidad de propagación $\pm{u}$,
\begin{equation}\partial_t^2f=u^2\,\partial_x^2f\label{waveeq}\end{equation} y se obtiene que
\begin{equation}\frac{1}{u^2}\partial_t^2f=\left(1-\frac{v^2}{u^2}\right)\partial_x^2f+\frac{2v}{u^2}\partial^2_{xt}f\label{inhwav}\end{equation} que en el caso $v\ll{u}$ se reduce a la ecuación original. En general en el caso de una onda material, es cierto que su velocidad de propagación dependerá del sistema de referencia: la solución general de la ec. (\ref{inhwav}) es
\begin{equation}f(x,t)=g\left(x+(v+u)t\right)+h\left(x+(v-u)t\right)\end{equation} de modo que la onda se propaga con velocidad $\pm{u}-v$; el dilema con la onda electromagnética es que ésta proviene de las ecuaciones dinámicas de los campos eléctrico y magnético, o de Maxwell, lo que las hace también no invariantes ante transformaciones Galileanas. Se puede ver directamente en las ecuaciones de Maxwell que el término $\partial_t$ es el verdugo, ya que $\partial_x\to\partial_x$ mientras que $\partial_t\to\partial_t-v\partial_x$; intuitivamente esto sugiere que el tiempo también debe cambiar en cierto modo al hacer un desplazamiento a velocidad constante.
[4] En 1887, Woldemar Voigt escribió la primera aproximación de las transformaciones de Lorentz (salvo una dilatación) en su artículo llamado simplemente 'Sobre el Principio Doppler', motivado por el efecto Doppler y un medio incompresible, que luego Lorentz establecería mejor como el éter, e imponiendo que la ec. (\ref{waveeq}) fuera invariante ante un observador en movimiento. Posteriormente Lorentz, Larmor y Poincaré siguieron haciendo avances, pero todos buscando acomodar y justificar su trabajo utilizando el éter. Así pues, aunque hoy se dan por sentado todas las consecuencias de la relatividad especial, es notable que la cuestión era realmente un rompecabezas.
[5] "Si viajara a la velocidad de la luz, mi trasero se vería estupendo... Einstein era famoso por su Gedankedank". La explicación a esta caricatura de xkcd está acá en inglés: http://www.explainxkcd.com/wiki/index.php/1233:_Relativity. El efecto Lampa-Terrell-Penrose hace que un observador en reposo perciba un objeto que se mueve a velocidad relativista como si estuviera rotado y con una muy ligera distorsión, de modo que si Einstein viajara a velocidad relativista mientras lo observas, podrías ver su trasero. Se explica también que la contracción de Lorentz la experimenta el objeto mismo (en este caso Einstein mismo, o más precisamente, su trasero) pero el observador externo no percibe realmente esta distorsión. Al parecer en la red hay poca información sobre este efecto y los artículos tanto de Lampa, Terrell y Penrose no son gratuitos, lo que es una pena.
[6] La solución de tipo agujero negro más simple es la de Schwarzschild, que vista por un observador en $r\to\infty$ es de la forma \begin{equation}ds^2=-c^2\left(1-\frac{r_s}{r}\right)dt^2+\left(1-\frac{r_s}{r}\right)^{-1}dr^2+r^2d\Omega^2\end{equation} y para rayos de luz $ds^2=0$, de modo que para cualquier latitud y longitud fijas (dada la simetría esférica de la métrica), \begin{equation}\left|\frac{dr}{dt}\right|=c\left|1-\frac{r_s}{r}\right|\end{equation} de modo que la velocidad de la luz es nula en el horizonte $r=r_s$, mientras que sigue siendo $c$ cuando $r\gg{r_s}$. Una situación análoga ocurrirá sin importar la métrica o en dónde se sitúe al observador.
[7] "Techo: Einstein vio a un hombre caer de un techo cercano sobre un montón de basura suave. El hombre luego dijo que no sintió la sensación de la gravedad mientras caía. Esa conversación, e investigación subsecuente, llevaron a Einstein a reconsiderar la gravedad Newtoniana."
Hasta acá la cosa parece bastante sencilla, pero este hecho tan simple tiene consecuencias que cambiaron para siempre nuestra percepción de la naturaleza del espacio y el tiempo con el nacimiento de la relatividad especial de Einstein en 1905, desde el hecho de que 'nada' viaja más rápido que la luz (entre otras causas por la llamada causalidad, aunque no lo discutiré acá) hasta algunos de los efectos más sorprendentes como que el espacio puede contraerse y el tiempo dilatarse.
La motivación de Einstein
Vale, pues usualmente se dice que esta 'invariancia' de la velocidad de la luz es un postulado de la relatividad especial, es decir, algo que se propone a priori y se emplea para poder formular la teoría, ¿pero entonces cómo es que se le ocurrió a Einstein proponer este postulado que dice que la velocidad de la luz es constante?
Greene también tiene un buen vídeo con la explicación: la teoría del electromagnetismo de Maxwell parecía sugerir que la velocidad de la luz es constante, lo que implicaba que el espacio y el tiempo se tendrían que comportar de manera distinta a la que nos es usual.
Pues... por ahí va la cosa.
Un ejercicio obligado en las clases de electromagnetismo clásico de licenciatura es el de encontrar, a partir de las ecuaciones de Maxwell, que los campos eléctrico y magnético satisfacen respectivas ecuaciones de onda que se propagan con una velocidad de poquitín menos de 300,000,000 m/s ([1]); estas ondas están sincronizadas en lo que se conoce clásicamente como radiación electromagnética, o simplemente, luz. Vale, entonces si éste es el valor de la velocidad de propagación de la luz en el marco de referencia en que lo deducen los alumnos, debería ser el mismo en cualquier otro (de hecho el marco 'elegido' implícitamente por los alumnos es desde un principio arbitrario); a fin de cuentas Galileo nos enseñó que las leyes de la física son las mismas independientemente de si las vemos en algún punto del espacio u otro o de si nos movemos con una velocidad constante de uno u otro modo.
El genio de Einstein para investigar esta cuestión sobre la velocidad de la luz fue precisamente el de tomar este principio de invariancia de las leyes físicas de Galileo en serio (que se llama principio de relatividad básicamente porque propone esta invariancia respecto a movimientos relativos entre marcos de referencia) y el de llevarlo a sus últimas consecuencias a pesar de los efectos poco intuitivos que acarreó en el entendimiento del espacio y el tiempo.
Cuando los físicos querían ver las ecuaciones de una onda electromagnética (o en general las ecuaciones de Maxwell) en otros sistemas de referencia, particularmente en uno que se mueve a velocidad constante, obtenían versiones distintas ([2]), lo que sugería que la luz no se propagaba siempre de la misma forma y con la misma velocidad, además de implicar que existían marcos de referencia privilegiados en los que las ecuaciones son todas bellas como Maxwell las describió originalmente [ignoro quiénes eran esos físicos, pero vaya, el dilema era esencialmente éste ;-)]. Los físicos por supuesto comenzaron a proponer soluciones a este problema, entre ellas la famosa solución del éter, que de hecho parecía bastante natural dada la idea de que una onda o vibración requiere de un medio para propagarse. Albert Michelson y Edward Morley realizaron un famoso experimento en 1887 en el que compararon la velocidad de la luz en distintas direcciones y básicamente encontraron que esta velocidad siempre es apróx. 300,000,000 m/s en cualquier dirección, descartando casi sin querer, la propuesta del éter. A la vista de estos resultados y de otros efectos relacionados como el efecto Doppler, el experimento de Fizeau y la aberración de la luz, grandes físicos como Poincaré, y antes Larmor y Lorentz, buscaron dar una explicación (algunos, como los mencionados, aferrándose al mismo éter) y de hecho hicieron grandes avances; de cualquier modo, no fue sino hasta Einstein cuando realmente se comprendieron las implicaciones de la invariancia de la velocidad de la luz y el principio de relatividad de Galileo en la naturaleza misma del espacio-tiempo.
La gran idea, y algo así como el 'sistema operativo', de la relatividad especial que dio solución al problema es la de las llamadas transformaciones de Lorentz, en la que precisamente trabajaron de manera fundamental (y en ese sentido hicieron avances) Poincaré, Larmor y Lorentz antes de Einstein. Una transformación en un sentido matemático no es más que una función que relaciona puntos de un espacio con otros puntos dentro del mismo espacio: las rotaciones, las traslaciones y los desplazamientos a velocidad constante de marcos de referencia son ejemplos de transformaciones y son éstas precisamente las transformaciones que mantienen la invariancia Galileana de las leyes físicas, por lo que a todas ellas juntas se les llama transformaciones Galileanas; el caso de los desplazamientos a velocidad constante es el que daba problemas cuando se quería considerar en el electromagnetismo (Greene explica el proceso matemático junto con la idea de simetría en este vídeo, aunque en el contexto del bosón de Higgs). En particular cuando uno considera estos desplazamientos a velocidad constante en las ecuaciones de onda del electromagnetismo, lo que se encuentra es que a velocidades bajas respecto a la de la luz, las ecuaciones se ven prácticamente igual a las originales pero no así cuando la velocidad de movimiento del marco de referencia respecto a la de la luz es alta ([3]). Cuando se habla de las transformaciones de Lorentz, se habla de rotaciones de marcos de referencia y de un tipo especial de transformación llamada boost que es análogo a los desplazamientos a velocidad constante; de este modo, las transformaciones de Lorentz se hacen cargo del problema generalizando los desplazamientos a velocidad constante con los boosts, que son válidos para desplazamientos a velocidades cercanas a la de la luz y que a su vez se reducen a los desplazamientos à la Galileo a velocidades bajas, lo que hace también que la relatividad especial sea una forma generalizada de la mecánica clásica y de este modo sea enteramente consistente.
El título de 'transformaciones de Lorentz' presuntamente lo acuñó Poincaré, pero bien podrían llamarse de Voigt-Larmor-Lorentz-Poincaré-Einstein ([4]) ;-) finalmente el éxito de Einstein fue que derivó y entendió estas transformaciones físicamente como relaciones espacio-temporales y dedujo las consecuencias revolucionarias (entre otras) de la dilatación temporal y la contracción espacial, que básicamente significaron que el espacio y el tiempo dejaran de ser algo absoluto y universal, mientras que la velocidad de la luz es exactamente la misma sin importar 'cómo se le vea'. Poco tiempo después otro desarrollo importante, también impulsado por Poincaré pero finalizado por Minkowski, fue el de que el espacio y el tiempo están íntimamente unidos en un espacio 4-dimensional, no Euclideano (o que puede pensarse con la coordenada temporal siendo imaginaria) que ahora llamamos espacio-tiempo (lo que a veces se atribuye directamente a Einstein), en donde los boosts son vistos como rotaciones espacio-temporales y en el que la relatividad especial (y el electromagnetismo) se formula naturalmente.
Finalmente algo tentador es pensar que la invariancia de la velocidad de la luz no debería ser algo que se propone a priori, sino que debe deducirse como consecuencia de la teoría. Y en cierto sentido es cierto, ya que puede obtenerse que la velocidad de la luz es finita únicamente a partir del principio de relatividad de Galileo y deducir que es constante del electromagnetismo clásico o de otras propiedades de simetría, pero la cuestión se torna en algo parecido a la discusión sobre si la primera ley de Newton es un caso particular de la segunda; el hecho es que ambas formas son válidas e incluso posiblemente el deducirlo es la mejor forma de hacerlo desde un punto de vista moderno (donde la luz es simplemente un campo más), de cualquier modo todo parece sencillo cuando se conoce de antemano cuál es la solución ;-)
 |
| ([5]) |
¿Y si la luz viaja en un medio?
Seguido se dice que la luz en un medio viaja más lentamente que en el vacío, pero esto así dicho nada más no es estrictamente correcto tomando en cuenta todo lo anterior y puede resultar engañoso; en general no es correcto tampoco decir que la luz puede detenerse o que puede hacerse disminuir su velocidad. Lo que sí se puede decir sin meter la pata es que se puede hacer que la luz recorra una cierta distancia en un tiempo menor o bien que la luz se puede propagar más lentamente en un medio; de cualquier modo la distinción puede resultar un poco pedante e incluso pasar desapercibida en la distinción que lleva implícita.
Como sea es relevante aclarar lo que sucede cuando la luz se propaga en un medio.
Clásicamente la luz está descrita por una onda electromagnética; así como uno obtiene el valor para la velocidad de propagación de la luz en el vacío, uno puede obtener una expresión para la velocidad de propagación de la luz en un medio dado (aunque de forma algo más complicada que en [1]) a través de las propiedades eléctricas y magnéticas que describen clásicamente al medio. La imagen macroscópica de esto último que uno tendría sería simplemente la de una onda viajando más lentamente al entrar en el medio.

Pensando a nivel atómico [sin invocar los detalles de la mecánica cuántica, es decir, pensando sólo en esferitas pequeñitas ;-) ], si se considera un medio con materia cualquiera [sólo no pensemos en nada exótico por el momento] que a fin de cuentas no está compuesto más que por átomos que a su vez no son más un núcleo y electrones, como es de imaginarse, pasa que la luz puede interactuar con la materia del medio, es decir, los átomos pueden 'absorber' la energía de la luz, lo que se traduce en 'excitar' o hacer vibrar a los electrones, que cuando se relajan nuevamente liberan esta energía en forma de otro paquete de ondas idéntico. Esto por supuesto no ocurre de manera instantánea, lo que generalizado a una gran cantidad de átomos, causa la ralentización que percibimos a nivel macroscópico. La idea, gráficamente, es ésta:

Es decir, es esta interacción con la materia lo que hace que la luz se propague más lentamente en el medio, pero esto no significa que la luz (que puede pensarse también como partículas sin masa, o fotones) deje de viajar a apróx. 300,000,000 m/s. Es por ello que el uso de la palabra propagación es en cierto sentido uno más certero. Si se quiere se puede apelar también a la vieja idea de que un átomo es en su gran mayoría espacio vacío, aunque esto tampoco es del todo correcto [uno puede seguirse con detalles y más detalles ;-) pero la idea principal es ésta].
Un caso exótico de un medio de propagación que resulta interesante en este sentido y que se ha vuelto accesible en tiempos recientes es el de los condensados de Bose-Einstein y la materia ultrafría. En este caso la idea de la absorción y re-emisión de luz también aplica aunque en una forma extrema, como en la llamada 'Transparencia Inducida por Electromagnetismo', logrando reducir la velocidad de propagación de la luz a hasta e.g. 17 m/s.
Otro caso que también es interesante es el de la radiación de Cherenkov, en la que una partícula cargada viaja a una velocidad mayor que la de la propagación de la luz en un medio, lo que ahora el lector debe entender que es enteramente posible respecto a la relatividad especial.
La velocidad de la luz cerca de un agujero negro
 |
| Imagen de un Agujero Negro en la película Interestelar |
Como sea, que la velocidad de la luz no sea constante para sistemas no-inerciales es una respuesta incompleta y no con mucho sentido: la cuestión es un tanto más sutil.
La idea clave de la relatividad general (la versión extendida de la relatividad especial que incluye gravedad) que impulsó a Einstein a formularla es el llamado Principio de Equivalencia. Lo que dice este principio es que un observador en reposo dentro de un campo gravitacional es indistinguible de uno acelerado en ausencia de gravedad (de ahí la importancia de que la relatividad especial pueda lidiar con aceleraciones). Esto tiene grandes consecuencias, entre ellas, que la gravedad, antes interpretada como una fuerza o interacción a distancia, no es más que un cambio en la propia geometría del espaciotiempo que altera las trayectorias inerciales acelerándolas. En particular, la gravedad no es más que la expresión de la curvatura del espaciotiempo (que Einstein además luego relacionó con el contenido de energía y materia del espacio).
Así pues, la velocidad de la luz no es siempre constante y puede cambiar cuando uno la mide en espacios curvos, o intuitivamente (en lenguaje Newtoniano, pues), cuando viaja dentro de un campo gravitacional...
¿Por qué tiene poco sentido?
En ausencia de gravedad, la teoría general de la relatividad se reduce al caso especial, en el que el espaciotiempo es plano. Otra forma de plantear el principio de equivalencia es diciendo que cualquier parte de un espaciotiempo curvo siempre ve localmente como un espaciotiempo plano. La palabra mágica local significa 'cerca' o a distancias 'cortas' del origen del observador. Los dos parafraseos del principio de equivalencia toman sentido con el ejemplo de un hombre (en la Tierra) dentro de un elevador cuyos cables se rompen súbitamente, quedando en caída libre, y que no puede distinguir su situación de la de, por ejemplo, un astronauta en el espacio; esto es, un hombre en caída libre experimenta exactamente lo mismo que un observador en el espacio libre de toda 'fuerza' externa. También sabemos por experiencia propia que a distancias cortas el mundo puede ser descrito bastante bien por la mecánica de Newton [o los ingenieros no podrían hacer nada de nada ;-) ], que a su vez utiliza geometría plana; lo único que nos recuerda que estamos en un campo gravitacional es el suelo de la Tierra misma que nos impide experimentar una caída libre todo el tiempo.
 |
| Una de las imágenes de General Relativity from A to Z del Perimeter Institute celebrando los 100 años de la Relatividad General ([7]) |
Matemáticamente la idea es que el espaciotiempo es algo así como una superficie 4-dimensional llamada variedad (en inglés manifold) que tiene la propiedad de que puede construirse con un montón de 'parches' planos, algo así como una piñata casera que se cubre con pedazos de papel 'planos'.

El decir, pues, que "la velocidad de la luz cambia cuando uno la mide en espacios curvos" es más una declaración de la geometría global del espaciotiempo curvo que de la realidad física acerca de la velocidad de la luz. En el caso de un agujero negro, el que la velocidad de la luz sea nula en el horizonte de eventos, es sólo una afirmación de las coordenadas que lo describen, y puede servir también para señalar que el horizonte de eventos es sólo una singularidad aparente o de coordenadas, y no una singularidad esencial, como la que se encuentra en el interior del agujero negro y en donde la relatividad general simplemente deja de ser válida.
Finalmente toda esta cuestión sirve de recordatorio de que las teorías físicas siempre (al menos hasta ahora) tienen un rango limitado de aplicabilidad, y al menos hasta donde he mostrado aquí, la invariancia de la velocidad de la luz es válida. De cualquier modo el trabajo de los físicos, y los científicos en general, es seguir expandiendo las fronteras de lo que entendemos de la naturaleza como válido ;-)
Las acotaciones
[1] De las ecuaciones de Maxwell en el vacío (sin fuentes)
\begin{align}\nabla\times\mathbf{E}&=-\partial_t\mathbf{B}\\\nabla\times\mathbf{B}&=\mu_0\epsilon_0\partial_t\mathbf{E}\\\nabla\cdot\mathbf{E}&=0\\\nabla\cdot\mathbf{B}&=0\end{align} empleando $\nabla\times(\nabla\times)=\nabla(\nabla\cdot)-\nabla^2$ en los rotacionales, se obtiene que $\left(\mu_0\epsilon_0\partial^2_t-\nabla^2\right)\begin{pmatrix}\mathbf{E}\\\mathbf{B}\end{pmatrix}=0$ de donde se identifica la velocidad de propagación $c=\frac{1}{\sqrt{\mu_0\epsilon_0}}\approx3\times10^8\,\text{m/s}$.
[2], [3] Se considera una transformacion Galileana en dos dimensiones (por simplicidad),
\begin{align}x&\to{x-vt}\\t&\to{t}\end{align} para una ecuación de onda clásica cualquiera con velocidad de propagación $\pm{u}$,
\begin{equation}\partial_t^2f=u^2\,\partial_x^2f\label{waveeq}\end{equation} y se obtiene que
\begin{equation}\frac{1}{u^2}\partial_t^2f=\left(1-\frac{v^2}{u^2}\right)\partial_x^2f+\frac{2v}{u^2}\partial^2_{xt}f\label{inhwav}\end{equation} que en el caso $v\ll{u}$ se reduce a la ecuación original. En general en el caso de una onda material, es cierto que su velocidad de propagación dependerá del sistema de referencia: la solución general de la ec. (\ref{inhwav}) es
\begin{equation}f(x,t)=g\left(x+(v+u)t\right)+h\left(x+(v-u)t\right)\end{equation} de modo que la onda se propaga con velocidad $\pm{u}-v$; el dilema con la onda electromagnética es que ésta proviene de las ecuaciones dinámicas de los campos eléctrico y magnético, o de Maxwell, lo que las hace también no invariantes ante transformaciones Galileanas. Se puede ver directamente en las ecuaciones de Maxwell que el término $\partial_t$ es el verdugo, ya que $\partial_x\to\partial_x$ mientras que $\partial_t\to\partial_t-v\partial_x$; intuitivamente esto sugiere que el tiempo también debe cambiar en cierto modo al hacer un desplazamiento a velocidad constante.
[4] En 1887, Woldemar Voigt escribió la primera aproximación de las transformaciones de Lorentz (salvo una dilatación) en su artículo llamado simplemente 'Sobre el Principio Doppler', motivado por el efecto Doppler y un medio incompresible, que luego Lorentz establecería mejor como el éter, e imponiendo que la ec. (\ref{waveeq}) fuera invariante ante un observador en movimiento. Posteriormente Lorentz, Larmor y Poincaré siguieron haciendo avances, pero todos buscando acomodar y justificar su trabajo utilizando el éter. Así pues, aunque hoy se dan por sentado todas las consecuencias de la relatividad especial, es notable que la cuestión era realmente un rompecabezas.
[5] "Si viajara a la velocidad de la luz, mi trasero se vería estupendo... Einstein era famoso por su Gedankedank". La explicación a esta caricatura de xkcd está acá en inglés: http://www.explainxkcd.com/wiki/index.php/1233:_Relativity. El efecto Lampa-Terrell-Penrose hace que un observador en reposo perciba un objeto que se mueve a velocidad relativista como si estuviera rotado y con una muy ligera distorsión, de modo que si Einstein viajara a velocidad relativista mientras lo observas, podrías ver su trasero. Se explica también que la contracción de Lorentz la experimenta el objeto mismo (en este caso Einstein mismo, o más precisamente, su trasero) pero el observador externo no percibe realmente esta distorsión. Al parecer en la red hay poca información sobre este efecto y los artículos tanto de Lampa, Terrell y Penrose no son gratuitos, lo que es una pena.
- Lampa: Wie erscheint nach der Relativitätstheorie ein bewegter Stab einem ruhenden Beobachter?.
- Penrose: The Apparent Shape of a Relativistically Moving Sphere.
- Terrell: Invisibility of the Lorentz contraction.

[6] La solución de tipo agujero negro más simple es la de Schwarzschild, que vista por un observador en $r\to\infty$ es de la forma \begin{equation}ds^2=-c^2\left(1-\frac{r_s}{r}\right)dt^2+\left(1-\frac{r_s}{r}\right)^{-1}dr^2+r^2d\Omega^2\end{equation} y para rayos de luz $ds^2=0$, de modo que para cualquier latitud y longitud fijas (dada la simetría esférica de la métrica), \begin{equation}\left|\frac{dr}{dt}\right|=c\left|1-\frac{r_s}{r}\right|\end{equation} de modo que la velocidad de la luz es nula en el horizonte $r=r_s$, mientras que sigue siendo $c$ cuando $r\gg{r_s}$. Una situación análoga ocurrirá sin importar la métrica o en dónde se sitúe al observador.
[7] "Techo: Einstein vio a un hombre caer de un techo cercano sobre un montón de basura suave. El hombre luego dijo que no sintió la sensación de la gravedad mientras caía. Esa conversación, e investigación subsecuente, llevaron a Einstein a reconsiderar la gravedad Newtoniana."
No comments:
Post a Comment